最近在工作中用到了这个算法,抽空做一个笔记。
判断一个点是否在多边形内部的问题在很多地方都会碰到,最常用的方法就是射线法。
射线法
以点P为端点,向左方作射线L,由于多边形是有界的,所以射线L的左端一定在多边形外,考虑沿着L从无穷远处开始自左向右移动,遇到和多边形的第一个交点的时候,进入到了多边形的内部,遇到第二个交点的时候,离开了多边形,…… 所以很容易看出当L和多边形的交点数目C是奇数的时候,P在多边形内,是偶数的话P在多边形外。
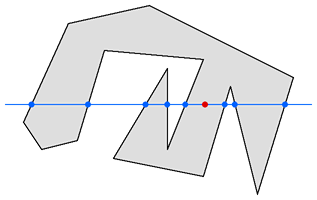
特殊情况
射线穿过多边形的顶点。
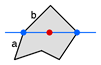
这个时候,这个顶点会被计算两次,这显然是不正确的。 解决方法是在射线上的顶点只在计算一次。为了达到这个目的,这里定义只有当一条边的一个端点在射线的下方,另一个端点在射线上或者射线的上方,我们才认为这条边与射线相交。这样一来,b边由于两个端点都在射线上或者在射线上方,因此被认为与射线不相交,而a边则与射线相交,那么这个顶点最终被计算了一次。
多边形的一条边在射线上。
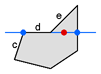
这时候我们参照上面第一种情况的方法,可以得出d边和e边都被认为与射线不相交,而c边与射线相交。这样c边和d边中间的顶点只被统计了一次,此时也可以得出点在多边形内的正确结论。
其他情况。
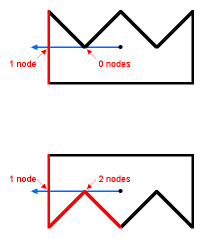
这是另外两种特殊的情况,可以看到我们参照上面的计算方法,依然可以得出正确的结论。
给定的点在多边形的边上。
在这种情况下,射线法的结果是不确定的,可能得到的结果是点在多边形内也可能是点在多边形外。可以根据实际的应用要求在实现算法中先判断点是否在多边形的边上。
算法实现
- C代码例子:
// Globals which should be set before calling this function:
//
// int polySides = how many corners the polygon has
// float polyX[] = horizontal coordinates of corners
// float polyY[] = vertical coordinates of corners
// float x, y = point to be tested
//
// (Globals are used in this example for purposes of speed. Change as
// desired.)
//
// The function will return YES if the point x,y is inside the polygon, or
// NO if it is not. If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
// by the "if" clause which surrounds it.
bool pointInPolygon() {
int i, j = polySides - 1 ;
bool oddNodes = NO ;
for (i = 0; i < polySides; i++) {
if (polyY[i] < y && polyY[j] >= y
|| polyY[j] < y && polyY[i] >= y) {
if (polyX[i] + (y-polyY[i]) / (polyY[j]-polyY[i]) * (polyX[j]-polyX[i]) < x) {
oddNodes =! oddNodes; }}
j = i; }
return oddNodes; }
这个C代码依次迭代多边形的每条边,判断是否与射线所在的直线相交(这里的相交表示边的两个端点一个在直线的下方,另个在直线上或者在直线上方)。如果边与直线相交,再判断边与直线的交点是否在测试点的左边(即射线上),这里的polyX[i]+(y-polyY[i])/(polyY[j]-polyY[i])*(polyX[j]-polyX[i])表示边与直线的交点的横坐标,可以通过线段所在直线的截距式方程和直线方程联立得出。
- 改进版:
// Globals which should be set before calling this function:
//
// int polySides = how many corners the polygon has
// float polyX[] = horizontal coordinates of corners
// float polyY[] = vertical coordinates of corners
// float x, y = point to be tested
//
// (Globals are used in this example for purposes of speed. Change as
// desired.)
//
// The function will return YES if the point x,y is inside the polygon, or
// NO if it is not. If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
// by the "if" clause which surrounds it.
bool pointInPolygon() {
int i, j = polySides - 1 ;
bool oddNodes = NO ;
for (i = 0; i < polySides; i++) {
if ((polyY[i] < y && polyY[j] >= y
|| polyY[j] < y && polyY[i] >= y)
&& (polyX[i] <= x || polyX[j] <= x)) {
if (polyX[i] + (y-polyY[i]) / (polyY[j]-polyY[i]) * (polyX[j]-polyX[i]) < x) {
oddNodes =! oddNodes; }}
j = i; }
return oddNodes; }
这份代码只比上面多了&& (polyX[i]<=x || polyX[j]<=x))这个判断条件,因为只有当边的两个端点中至少有一个横坐标小于给定点的横坐标,那么这条边与直线的交点才会在给定点的左边。
- 另一个改进版,用异或操作符取代了if语句:
// Globals which should be set before calling this function:
//
// int polySides = how many corners the polygon has
// float polyX[] = horizontal coordinates of corners
// float polyY[] = vertical coordinates of corners
// float x, y = point to be tested
//
// (Globals are used in this example for purposes of speed. Change as
// desired.)
//
// The function will return YES if the point x,y is inside the polygon, or
// NO if it is not. If the point is exactly on the edge of the polygon,
// then the function may return YES or NO.
//
// Note that division by zero is avoided because the division is protected
// by the "if" clause which surrounds it.
bool pointInPolygon() {
int i, j=polySides-1 ;
bool oddNodes=NO ;
for (i=0; i<polySides; i++) {
if ((polyY[i] < y && polyY[j] >= y
|| polyY[j] < y && polyY[i] >= y)
&& (polyX[i] <= x || polyX[j] <= x)) {
oddNodes ^= (polyX[i]+(y-polyY[i]) / (polyY[j] - polyY[i]) * (polyX[j]-polyX[i]) < x); }
j = i; }
return oddNodes; }